תיאוריה נוספת
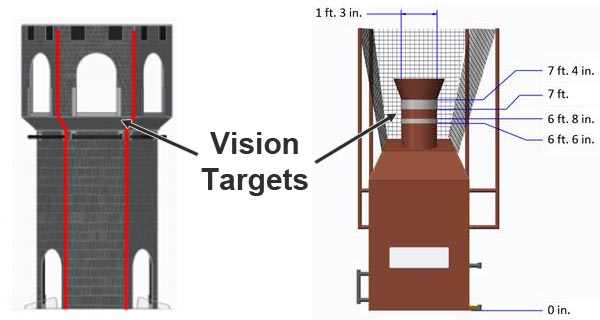
מטרות ראייה
מעצבי משחקי FRC ממקמים לעתים קרובות "מטרות ראייה" מחזירות אור על המגרש במיקומים אסטרטגיים. מטרות ראייה אלו עשויות בדרך כלל מסרט רטרו-רפלקטיבי. לאלמנטי ניקוד מרכזיים יש בדרך כלל מטרות ראייה שניתן להשתמש בהן לכיוון אוטומטי. למטה תוכלו לראות שתי דוגמאות של מטרות ראייה ממשחקי FRC של 2016 ו-2017.
למטרות ראייה רטרו-רפלקטיביות אלו יש תכונה שימושית מאוד: כאשר מאירים עליהן אור, הוא יוחזר ישירות למקור האור. זו הסיבה ש-Limelight מצויד בנורות LED ירוקות בהירות סביב עדשת המצלמה. על ידי הגדרת חשיפת המצלמה לנמוכה מאוד תוך פליטת אור ירוק בהיר לכיוון המטרה, אנו יכולים לקבל תמונה שהיא בעיקר שחורה עם מטרת ראייה ירוקה בהירה. זה הופך את משימת זיהוי המטרה לקלה יחסית.
כאן תוכלו לראות דוגמה לתמונה אידיאלית. שימו לב כיצד כמעט כל הפרטים בתמונה נעלמו בגלל הגדרת החשיפה הנמוכה אך הסרט הרטרו-רפלקטיבי בולט בבהירות.

סינון סף
סינון סף הוא המרכיב הקריטי הבא ברוב אלגוריתמי מעקב הראייה של FRC. זוהי פעולה של לקיחת תמונה והשלכת כל פיקסל שאינו בטווח צבעים מסוים. התוצאה של סינון סף היא בדרך כלל תמונה חד-ממדית שבה פיקסל הוא "דלוק" או "כבוי". סינון סף עובד היטב על תמונות שנלכדו באמצעות האסטרטגיה שלעיל (חשיפה נמוכה, תמונה כהה מאוד עם מטרת ראייה מוארת בבהירות).
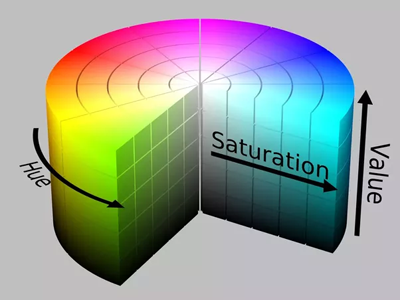
Limelight מבצע סינון סף במרחב הצבעים HSV (גוון-רוויה-ערך). ייתכן שאתם רגילים לחשוב על צבעים במרחב הצבעים RGB (אדום-ירוק-כחול). HSV הוא פשוט דרך אחרת לייצג צבע, בדומה לאופן שבו קואורדינטות קרטזיות או קואורדינטות קוטביות יכולות לשמש לתיאור מיקומים. הסיבה שאנו משתמשים במרחב הצבעים HSV היא שניתן להשתמש בגוון כדי לבחור בצורה מדויקת מאוד את הצבע הירוק שנורות ה-LED של Limelight פולטות.
חיוני להתאים את הגדרות סינון הסף שלכם כדי להסיר כמה שיותר מהתמונה. תקבלו את התוצאות הטובות ביותר אם תמטבו כל שלב בצינור הראייה שלכם לפני המעבר לשלב הבא. התמונה הבאה מציגה את ההבדל בין סינון סף לא נכון לנכון:

לפעמים דברים כמו תאורת תקרה או חלונות בזירה יכולים להיות קשים להסרה מהתמונה באמצעות סינון סף, מה שמביא אותנו לשלב הבא.
סינון קווי מתאר
לאחר סינון הסף, צינור הראייה של Limelight מייצר קבוצה של קווי מתאר לתמונה. קו מתאר הוא עקומה המקיפה קבוצה רציפה של פיקסלים. לפעמים דברים כמו תאורת תקרה, לוחות תוצאות של זירה, חלונות ודברים אחרים יכולים לעבור את שלב סינון הסף. כאן סינון קווי המתאר הופך לשימושי. המטרה היא להסיר כל קווי מתאר שאנו יודעים שאינם המטרה שאנו מעוניינים בה.
המסנן הראשון והקל ביותר של קווי מתאר הוא להתעלם מכל קווי מתאר שקטנים ממה שמטרת הראייה שלנו נראית ממרחק הניקוד שלנו. כל דבר קטן מגודל זה הוא ברור משהו רחוק יותר ויש להתעלם ממנו. זה נקרא סינון שטח.
למטרות הראייה של FRC יש לעתים קרובות תכונה גיאומטרית כלשהי שניתן לנצל כדי לעזור לנו לסנן קווי מתאר. לדוגמה, אם למטרת הראייה יש יחס רוחב-גובה רחב, אנו יכולים לסנן כל קווי מתאר שאינם רחבים:

עם זאת, זכרו שהמצלמה שלכם עשויה להסתכל על המטרה מזווית מוזרה. זה יכול להשפיע באופן דרמטי על יחס הרוחב-גובה של קו המתאר שלה. הקפידו לבדוק את ההגדרות שלכם ממגוון זוויות כדי להבטיח שאתם לא מסננים באגרסיביות יתר ובסופו של דבר מתעלמים ממטרת הראייה!

מטרת התמונה הבאה מעניינת מאוד. זו אחת ממטרות הראייה המעוצבות הכי טוב ב-FRC (לדעתנו). Limelight מחשב אוטומטית ערך הנקרא מלאות של קו מתאר. מלאות היא היחס בין שטח הפיקסלים של קו המתאר לשטח הקמור שלו. לצורה הספציפית הזו יש מלאות נמוכה מאוד וכמעט אף פעם לא רואים תאורת תקרה, חלונות וכו' עם מלאות כל כך נמוכה. אז אתם יכולים לסנן ביעילות רבה את קווי המתאר הלא רצויים אם מטרת הראייה שלכם נראית כמו זו.

ל-Limelight יש אפשרויות רבות לסינון קווי מתאר. אתם יכולים להשתמש באפשרויות אלו יחד עם מה שאתם יודעים על תכונות הגיאומטריה של מטרת הראייה הספציפית שאתם מנסים לעקוב אחריה.
כרגע, אם מספר קווי מתאר עוברים את אפשרויות הסינון שלכם, קו המתאר הגדול ביותר נבחר. בנוסף, הצינור מעדיף "להינעל" על קווי מתאר באמצעות היסטרזיס. זו תכונה שעוזרת למנוע הבהוב בין מטרות דומות.
מפיקסלים לזוויות
התוצאה הסופית של צינור הראייה היא מיקום פיקסל של קו המתאר הטוב ביותר בתמונה. עבור רוב המשחקים, אנו יכולים פשוט לכוון למרכז קו המתאר. לפעמים �שימושי גם לכוון למרכז העליון או לנקודה אחרת אך בעצם יש לנו קואורדינטת פיקסל למקום שאליו אנו רוצים לכוון. כדי לחשב את הזוויות למטרה זו, אנו צריכים להשתמש בקצת טריגונומטריה.
ראשית אנו מניחים שיש לנו מצלמת "חור סיכה" מושלמת. בפועל זה יכול להיות רחוק מהאמת אך המצלמה של Limelight קרובה מאוד. (עדשת עין דג תהיה רחוקה מאידיאל זה כדוגמה נגדית.)
למצלמת Limelight יש שדה ראייה אופקי של 54 מעלות ושדה ראייה אנכי של 41 מעלות. היא לוכדת תמונות ברזולוציה של 320x240. אנו מניחים שמרכז התמונה הוא הציר האופטי של המצלמה (כך שזוויות x ו-y עבור מיקום זה הן 0,0). בהינתן ערכים ידועים אלו, אנו יכולים להשתמש בקצת טריגונומטריה כדי לחשב את הזוויות עבור כל פיקסל בתמונה.
התרשים למטה מציג נקודת מטרה לדוגמה שעבורה אנו רוצים לחשב זוויות. קואורדינטות פיקסל מתחילות בפינה השמאלית העליונה של התמונה וחיוביות ימינה ולמטה.
![]()
הצעד הראשון שלנו יהיה להמיר מקואורדינטות פיקסל לקואורדינטות דו-ממדיות מנורמלות כאשר 0,0 הוא מרכז התמונה ו-1.0:
(px, py) = קואורדינטות פיקסל, 0,0 הוא הפינה השמאלית העליונה, חיובי למטה וימינה
(nx, ny) = קואורדינטות פיקסל מנורמלות, 0,0 הו�א המרכז, חיובי ימינה ולמעלה
nx = (1/160) * (px - 159.5)
ny = (1/120) * (119.5 - py)
לאחר מכן אנו מגדירים מישור ראייה דמיוני ומחשבים את גודלו. לפשטות, אנו יכולים לבחור למקם מישור זה ביחידה אחת מול מיקום המצלמה. הנה מבט מלמעלה על המצלמה. המטרה שלנו היא לחשב את רוחב וגובה מישור הראייה מכיוון שערכים אלו ישמשו לחישוב הזוויות מאוחר יותר:
![]()
בהינתן מרחק של יחידה אחת ושדה ראייה אופקי ואנכי ידוע, אנו יכולים לחשב את גודל מלבן מישור הראייה בנוסחאות הבאות:
vpw = 2.0*tan(horizontal_fov/2)
vph = 2.0*tan(vertical_fov/2)
באמצעות שני ערכים אלו, אנו יכולים כעת להמיר בין קואורדינטות פיקסל מנורמלות לקואורדינטות מישור ראייה באמצעות כפל פשוט.
x = vpw/2 * nx;
y = vph/2 * ny;
זכרו שבחרנו למקם את מישור הראייה שלנו במרחק של 1.0. כעת יש לנו את כל מה שאנו צריכים כדי לחשב את הזוויות לנקודת המטרה.
![]()
tan(ax) = x / 1
tan(ay) = y / 1
ax = atan2(x, 1)
ay = atan2(y, 1)