Teoría Adicional
Objetivos de Visión
Los diseñadores del juego FRC a menudo colocan "objetivos de visión" reflectantes en el campo en ubicaciones estratégicas. Estos objetivos de visión generalmente están hechos de cinta retrorreflectante. Los elementos de puntuación principales generalmente tienen objetivos de visión que pueden usarse para apuntar automáticamente. A continuación puedes ver dos ejemplos de algunos de los objetivos de visión de los juegos FRC de 2016 y 2017.
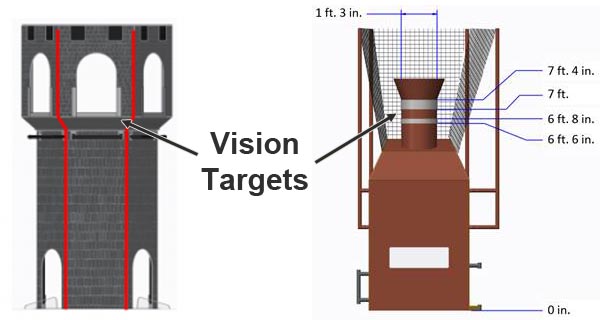
Estos objetivos de visión retrorreflectantes tienen una propiedad muy útil: cuando se les proyecta luz, esta se refleja directamente de vuelta a la fuente de luz. Por eso Limelight tiene LEDs verdes brillantes alrededor de su lente de cámara. Al configurar la exposición de la cámara muy baja mientras se emite una luz verde brillante hacia el objetivo, podemos adquirir una imagen que es mayormente negra con un objetivo de visión verde brillante. Esto hace que la tarea de adquirir el objetivo sea relativamente fácil.
Aquí puedes ver un ejemplo de la imagen ideal. Observa cómo casi todo el detalle en la imagen ha desaparecido debido a la configuración de baja exposición, pero la cinta retrorreflectante destaca brillantemente.

Umbralización
La umbralización es el siguiente componente crítico de la mayoría de los algoritmos de seguimiento de visión FRC. Es el acto de tomar una imagen y descartar cualquier píxel que no esté en un rango de color específico. El resultado de la umbralización es generalmente una imagen unidimensional en la que un píxel está "encendido" o "apagado". La umbralización funciona muy bien en imágenes que se capturan usando la estrategia anterior (baja exposición, imagen muy oscura con un objetivo de visión brillantemente iluminado).
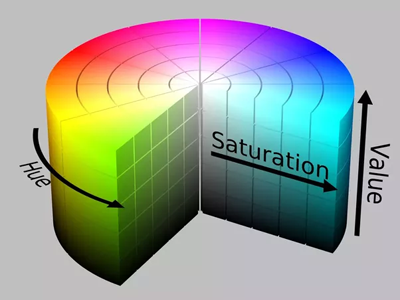
Limelight realiza la umbralización en el espacio de color HSV (Tono-Saturación-Valor). Puede que estés acostumbrado a pensar en los colores en el espacio de color RGB (Rojo-Verde-Azul). HSV es simplemente otra forma de representar el color, similar a cómo las coordenadas cartesianas o las coordenadas polares pueden usarse para describir posiciones. La razón por la que usamos el espacio de color HSV es que el Tono puede usarse para seleccionar muy precisamente el color verde que emiten los LEDs de Limelight.
Es crítico ajustar tu configuración de umbralización para eliminar tanto como puedas de la imagen. Obtendrás los mejores resultados si optimizas cada etapa de tu pipeline de visión antes de pasar a la siguiente etapa. La siguiente imagen muestra la diferencia entre una umbralización incorrecta y correcta:

A veces cosas como luces del techo o ventanas en una arena pueden ser difíciles de eliminar de la imagen usando umbralización, lo que nos lleva a la siguiente etapa.
Filtrado de Contornos
Después de la umbralización, el pipeline de visión de Limelight genera un conjunto de contornos para la imagen. Un contorno es una curva que rodea un conjunto contiguo de píxeles. A veces cosas como luces del techo, marcadores de arena, ventanas y otras cosas pueden pasar la etapa de umbralización. Aquí es donde el filtrado de contornos se vuelve útil. El objetivo es eliminar cualquier contorno que sepamos que no es el objetivo que nos interesa.
El primer y más fácil filtro de contornos es ignorar cualquier contorno que sea más pequeño de lo que nuestro objetivo de visión se ve desde nuestra distancia de puntuación. Cualquier cosa más pequeña que ese tamaño es obviamente algo más lejano y debe ignorarse. Esto se llama filtrado por área.
Los objetivos de visión FRC a menudo tienen alguna propiedad geométrica que puede explotarse para ayudarnos a filtrar contornos. Por ejemplo, si el objetivo de visión tiene una relación de aspecto ancha, podemos filtrar cualquier contorno que no sea ancho:

Sin embargo, ten en cuenta que tu cámara puede estar mirando el objetivo desde un ángulo extraño. Esto puede afectar drásticamente la relación de aspecto de su contorno. ¡Asegúrate de probar tu configuración desde una variedad de ángulos para garantizar que no filtres demasiado agresivamente y termines ignorando el objetivo de visión!

Este siguiente objetivo de imagen es muy interesante. Es uno de los objetivos de visión mejor diseñados en FRC (en nuestra opinión). Limelight calcula automáticamente un valor llamado plenitud de un contorno. La plenitud es la proporción entre el área en píxeles del contorno y su área convexa. Esta forma particular tiene una plenitud muy baja y casi nunca ves luces del techo, ventanas, etc. con una plenitud tan baja. Así que puedes filtrar muy efectivamente los contornos no deseados si tu objetivo de visión se ve como este.

Limelight tiene muchas opciones para filtrar contornos. Puedes usar estas opciones junto con lo que sabes sobre las propiedades geométricas del objetivo de visión particular que estás tratando de rastrear.
Actualmente, si múltiples contornos pasan a través de tus opciones de filtrado, se elige el contorno más grande. Además, el pipeline prefiere "bloquearse" en contornos usando histéresis. Esta es una característica que ayuda a prevenir el parpadeo entre objetivos similares.
De Píxeles a Ángulos
El resultado final del pipeline de visión es una ubicación en píxeles del mejor contorno en la imagen. Para la mayoría de los juegos, simplemente podemos apuntar al centro del contorno. A veces también es útil apuntar al centro superior o algún otro punto, pero esencialmente tenemos una coordenada de píxel para donde queremos apuntar. Para calcular los ángulos hacia este objetivo, necesitamos usar un poco de trigonometría.
Primero asumimos que tenemos una cámara "pinhole" perfecta. En la práctica esto puede estar lejos de la verdad, pero la cámara de Limelight está muy cerca. (Un lente ojo de pez estaría lejos de este ideal como contraejemplo.)
La cámara de Limelight tiene un campo de visión horizontal de 54 grados y un campo de visión vertical de 41 grados. Captura imágenes a una resolución de 320x240. Asumimos que el centro de la imagen es el eje óptico de la cámara (por lo que los ángulos x e y para esa ubicación son 0,0). Dados estos valores conocidos, podemos usar un poco de trigonometría para calcular los ángulos para cualquier píxel en la imagen.
El diagrama a continuación muestra un punto objetivo de ejemplo para el cual queremos calcular ángulos. Las coordenadas de píxeles comienzan en la esquina superior izquierda de la imagen y son positivas hacia la derecha y hacia abajo.
![]()
Nuestro primer paso será convertir de coordenadas de píxeles a coordenadas 2D normalizadas donde 0,0 es el centro de la imagen y 1.0:
(px, py) = coordenadas de píxeles, 0,0 es la esquina superior izquierda, positivo hacia abajo y hacia la derecha
(nx, ny) = coordenadas de píxeles normalizadas, 0,0 es el centro, positivo hacia la derecha y hacia arriba
nx = (1/160) * (px - 159.5)
ny = (1/120) * (119.5 - py)
A continuación definimos un plano de vista imaginario y calculamos su tamaño. Por simplicidad, podemos elegir colocar este plano a 1.0 unidad frente a la ubicación de la cámara. Aquí hay una vista mirando hacia abajo sobre la cámara. Nuestro objetivo es calcular el ancho y alto del plano de vista ya que esos valores se usarán para calcular los ángulos más tarde:
![]()
Dada una distancia de 1.0 unidad y un fov horizontal y vertical conocido, podemos calcular el tamaño del rectángulo del plano de vista con las siguientes fórmulas:
vpw = 2.0*tan(horizontal_fov/2)
vph = 2.0*tan(vertical_fov/2)
Usando estos dos valores, ahora podemos convertir entre coordenadas de píxeles normalizadas y coordenadas del plano de vista usando una simple multiplicación.
x = vpw/2 * nx;
y = vph/2 * ny;
Recuerda que elegimos que nuestro plano de vista esté posicionado a una distancia de 1.0. Ahora tenemos todo lo que necesitamos para calcular los ángulos hacia el punto objetivo.
![]()
tan(ax) = x / 1
tan(ay) = y / 1
ax = atan2(x, 1)
ay = atan2(y, 1)