Aller au contenu principal

Estimation de la Distance

Utilisation d'une Caméra à Angle Fixe​

Si votre caméra de suivi de vision est montée sur votre robot de telle sorte que l'angle entre le plan du sol et sa ligne de visée ne change pas, alors vous pouvez utiliser cette technique pour calculer très précisément la distance jusqu'à une cible. Vous pouvez ensuite utiliser cette valeur de distance pour soit faire avancer ou reculer votre robot afin d'atteindre la portée parfaite, soit ajuster la puissance d'un mécanisme de lancement.

Voir le diagramme ci-dessous. Dans ce contexte, toutes les variables sont connues : la hauteur de la cible (h2) est connue car c'est une propriété du terrain. La hauteur de votre caméra au-dessus du sol (h1) est connue et son angle de montage est connu (a1). Le Limelight (ou votre système de vision) peut vous indiquer l'angle y vers la cible (a2).

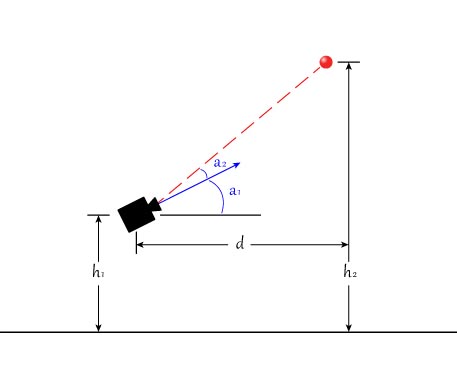
Estimation de Distance

Nous pouvons résoudre pour d en utilisant l'équation suivante :

tan(a1+a2) = (h2-h1) / d

"d = (h2-h1) / tan(a1+a2)"

La fonction "tan" attend généralement une entrée mesurée en radians. Pour convertir une mesure d'angle de degrés en radians, multipliez par (3.14159/180.0). Voir l'exemple de code complet ci-dessous.

    NetworkTable table = NetworkTableInstance.getDefault().getTable("limelight");
    NetworkTableEntry ty = table.getEntry("ty");
    double targetOffsetAngle_Vertical = ty.getDouble(0.0);

    // de combien de degrés votre limelight est-il incliné vers l'arrière par rapport à la verticale parfaite ?
    double limelightMountAngleDegrees = 25.0; 

    // distance du centre de la lentille du Limelight au sol
    double limelightLensHeightInches = 20.0; 

    // distance de la cible au sol
    double goalHeightInches = 60.0; 

    double angleToGoalDegrees = limelightMountAngleDegrees + targetOffsetAngle_Vertical;
    double angleToGoalRadians = angleToGoalDegrees * (3.14159 / 180.0);

    // calculer la distance
    double distanceFromLimelightToGoalInches = (goalHeightInches - limelightLensHeightInches) / Math.tan(angleToGoalRadians);

Lors de l'utilisation de cette technique, il est important de choisir soigneusement l'angle de montage de votre caméra. Vous voulez pouvoir voir la cible à la fois lorsque vous êtes trop près et trop loin. Vous ne voulez pas non plus que cet angle change, donc montez-la solidement et évitez d'utiliser des fentes dans votre géométrie de montage.

Si vous avez du mal à déterminer quel est l'angle a1, vous pouvez également utiliser l'équation ci-dessus pour résoudre pour a1. Placez simplement votre robot à une distance connue (en mesurant depuis la lentille de votre caméra) et résolvez la même équation pour a1.

Dans le cas où votre cible est à peu près à la même hauteur que votre caméra, cette technique n'est pas utile.

Utilisation de l'Aire pour Estimer la Distance​

Une autre façon simple d'estimer la distance est d'utiliser l'aire du contour que vous suivez. C'est une méthode très simple à implémenter mais elle ne donne pas des résultats extrêmement précis. Tout ce que vous avez à faire est de pointer votre caméra de vision vers la cible depuis une distance connue et de noter l'aire du blob. Assurez-vous d'utiliser une représentation précise de la cible de vision du vrai terrain et assurez-vous de pointer vers elle depuis votre position de tir souhaitée. Vous pouvez ensuite faire cela depuis quelques distances différentes et créer un tableau à partir de ces valeurs. En 2016, nous avons utilisé cette méthode pour ajuster la visée de notre tourelle à 2 axes en fonction de notre distance par rapport au but.