Saltar al contenido principal

Estimación de Distancia

Usando una Cámara con Ángulo Fijo​

Si la cámara de seguimiento de visión está montada en tu robot de tal manera que el ángulo entre el plano del suelo y su línea de visión no cambia, entonces puedes usar esta técnica para calcular con mucha precisión la distancia a un objetivo. Luego puedes usar este valor de distancia para mover tu robot hacia adelante y atrás para obtener el rango perfecto o ajustar la potencia de un mecanismo de lanzamiento.

Observa el diagrama a continuación. En este contexto, todas las variables son conocidas: la altura del objetivo (h2) es conocida porque es una propiedad del campo. La altura de tu cámara sobre el suelo (h1) es conocida y su ángulo de montaje es conocido (a1). El Limelight (o tu sistema de visión) puede indicarte el ángulo y hacia el objetivo (a2).

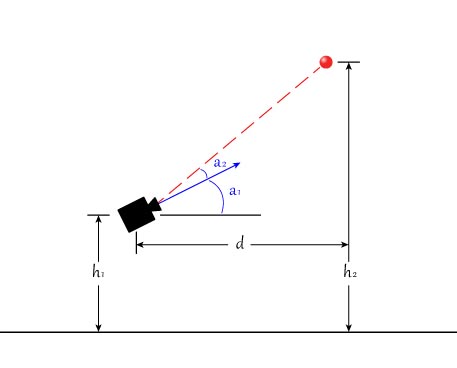
Estimación de Distancia

Podemos resolver para d usando la siguiente ecuación:

tan(a1+a2) = (h2-h1) / d

"d = (h2-h1) / tan(a1+a2)"

La función "tan" generalmente espera una entrada medida en radianes. Para convertir una medida de ángulo de grados a radianes, multiplica por (3.14159/180.0). Consulta el ejemplo de código completo a continuación.

    NetworkTable table = NetworkTableInstance.getDefault().getTable("limelight");
    NetworkTableEntry ty = table.getEntry("ty");
    double targetOffsetAngle_Vertical = ty.getDouble(0.0);

    // ¿cuántos grados hacia atrás está rotado tu limelight desde perfectamente vertical?
    double limelightMountAngleDegrees = 25.0; 

    // distancia desde el centro del lente del Limelight hasta el suelo
    double limelightLensHeightInches = 20.0; 

    // distancia desde el objetivo hasta el suelo
    double goalHeightInches = 60.0; 

    double angleToGoalDegrees = limelightMountAngleDegrees + targetOffsetAngle_Vertical;
    double angleToGoalRadians = angleToGoalDegrees * (3.14159 / 180.0);

    // calcular distancia
    double distanceFromLimelightToGoalInches = (goalHeightInches - limelightLensHeightInches) / Math.tan(angleToGoalRadians);

Al usar esta técnica es importante elegir cuidadosamente el ángulo de montaje de tu cámara. Quieres poder ver el objetivo tanto cuando estás demasiado cerca como demasiado lejos. También no quieres que este ángulo cambie, así que móntala de forma segura y evita usar ranuras en la geometría de montaje.

Si tienes problemas para determinar cuál es el ángulo a1, también puedes usar la ecuación anterior para resolver a1. Simplemente coloca tu robot a una distancia conocida (midiendo desde el lente de tu cámara) y resuelve la misma ecuación para a1.

En el caso donde tu objetivo está casi a la misma altura que tu cámara, esta técnica no es útil.

Usando el Área para Estimar Distancia​

Otra forma simple de estimar la distancia es usar el área del contorno que estás rastreando. Este es un método muy simple de implementar pero no te da resultados extremadamente precisos. Todo lo que haces es apuntar tu cámara de visión al objetivo desde una distancia conocida y tomar nota del área del blob. Asegúrate de estar usando una representación precisa del objetivo de visión del campo real y asegúrate de estar apuntando desde tu ubicación de disparo deseada. Luego puedes hacer esto desde algunas distancias diferentes y crear una tabla con estos valores. En 2016 usamos este método para ajustar la puntería de nuestra torreta de 2 ejes basándonos en qué tan lejos estábamos del objetivo.